Ley de Gauss.
NAVARRRO NICOLL
Johann Carl Friedrich Gauss fue un matemático notable, astrónomo geodesta y físico alemán que contribuyo significativamente en la ciencia con la demostración de su teorema, más conocida como “Ley de Gauss" que nos permite calcular de una forma simple el modulo del campo magnético, cuando conocemos la distribución de cargas con simetrías esféricas o cilíndricas.
Ahora mencionaremos al Flujo del campo magnético a través de cualquier superficie cerrada es igual a la carga contenida dentro de la superficie dividida por una constante Eo.
Imagine un elemento de aérea dA sobre una superficie de forma arbitraria, si el campo eléctrico en este elemento es B, el flujo magnético a través del elemento es B.dA, donde dA es un vector perpendicular a la superficie y que tiene una magnitud igual al área da. Debido a eso, el flujo magnético total a través de la superficie es la integral de BxdA. (Serway-Jewett. 2009. pàg.850)
A continuación mencionaremos al campo magnético y sus aplicaciones que es de suma importancia para poder comprender la ley de Gauss, el cual tiene dos casos:
● Si el campo es paralelo al plano su ángulo será de 90° y su flujo a través del plano es igual a cero.
● Si el campo es perpendicular al plano, entonces so ángulo será 0°.
Una de las aplicaciones del campo magnético, es del imán de barra.
Serway-lewett(2009)sostiene: “Las líneas de campo magnético de un imán de barra forman espiras cerradas. Advierta que el flujo magnético neta a través de una superficie cerrada que rodea a uno de los polos es igual a cero” (p.851).
Según Serway-Lewett(2009), llegamos a la conclusión que el flujo eléctrico a través de una superficie cerrada que rodea a una carga neta es proporcional a dicha carga (ley de Gauss, pàg.182).
En síntesis, tenemos claro que si hablamos de flujo asociamos rápidamente con el campo magnético, y el ejemplo más claro de campo magnético es su aplicación, los imanes de barras, donde salen a la superficie un número de líneas que dependen únicamente de la carga neta que se encuentra en su interior.
Referencias:
- Libro Serway-lewett.
- Monografias Electrostáticas.
NAVARRRO NICOLL
Flujo Eléctrico.
NAVARRRO NICOLL
El flujo eléctrico es base importante para entender la ley de Gauss. El flujo eléctrico es una cantidad escalar que expresa una medida del campo eléctrico que atraviesa una superficie. Se origina en cargas positivas y terminan en cargas negativas, en ausencia de cargas negativas termina en infinito
Consideremos cierto campo vectorial F en el espacio, y en ese espacio cierta superficie cerrada S arbitraria. Serway-Lewett(2009)afirma: “Cuando la superficie está siendo atravesada encierra alguna carga neta, el número total de líneas que pasan por S es proporcional a la carga neta que está en el interior de ella”.(p.852).
Cabe recalcar que en cualquier superficie o plano existe un vector normal, del cual hablaremos a continuación. El vector normal lo llamaremos n a la superficie es el que apunta de forma perpendicular, y hacia afuera de volumen definido por la superficie cerrada.
Existen analogías con un fluido, y tenemos a “v” que es el campo de velocidad del fluido, con lo que se concluye 3 casos:
El flujo es el volumen del fluido que atraviesa la superficie por unidad de tiempo.
● Podemos definir el flujo de F a través de esa superficie como:
● Donde la integral es sobre S, todo la superficie. Si se trata del campo eléctrico Ex(r) entonces el flujo eléctrico a través de esa superficie S es:
En síntesis, como el campo es proporcional al número de líneas de fuerza por unida de área, el flujo eléctrico es proporcional al número de líneas de fuerza que atraviesan a la superficie.A fin de poder generalizar y poder considerar superficies que no sean perpendiculares en todos los puntos al campo.
Referencias:
- Libro Serway-lewett.
- Monografias Electrostáticas.
NAVARRRO NICOLL
Cascaron esférico de Flujo Eléctrico.
NAVARRRO NICOLL
Para este tema se aplica la Ley de Gauss que se vio anteriormente a un cascarón esférico con carga distribuida uniformemente sobre su superficie, para calcular el campo eléctrico en un punto interior y exterior al cascarón.
“Considerando una superficie gausiana en forma de una esfera de radio r, el campo eléctrico tiene la misma magnitud en cada punto de la esfera y está dirigido hacia afuera. El flujo eléctrico es por tanto el campo eléctrico multiplicado por el área de la esfera.”(Física 2, 2005, pág. 123).
El campo eléctrico dentro del cascarón esférico es igual a cero. El campo eléctrico fuera del cascarón esférico tiene la misma expresión de campo eléctrico de una carga puntual aislada.
El teorema de Gauss dice: “El flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga encerrada en el interior de dicha superficie dividida entre εo.”
En síntesis, el cascaron esférico es un área que se forma de manera natural en todo objeto cargado eléctricamente, el cual se puede cargar natural o intencionalmente este campo es fundamental y es una viable aplicación para la ley de gauss ya que en ella se encuentran todas las fuerzas que podrían ejercerse sobre un cuerpo.
- Libro Física 2.
- www. Física lab. com
NAVARRRO NICOLL






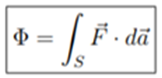



No hay comentarios.:
Publicar un comentario